Scalene Triangle
- What is A Scalene Triangle?
- Types of Scalene Triangles
- Solved Examples on Scalene Triangle
- Practice Problems on Scalene Triangle
- Frequently Asked Questions on Scalene Triangle
Introduction to Scalene Triangle:
A scalene triangle is a type of triangle where all three sides have different lengths. It is a fundamental concept in geometry and plays an important role in various mathematical and real-life applications. In this article, we will delve into the definition, types, examples, facts, and frequently asked questions related to scalene triangles.
Definition of a Scalene Triangle:
A scalene triangle is a polygon made up of three sides of different lengths. It is characterized by the fact that none of its sides or angles are equal. In other words, all three sides of a scalene triangle have different measures, and all three angles are also unequal.
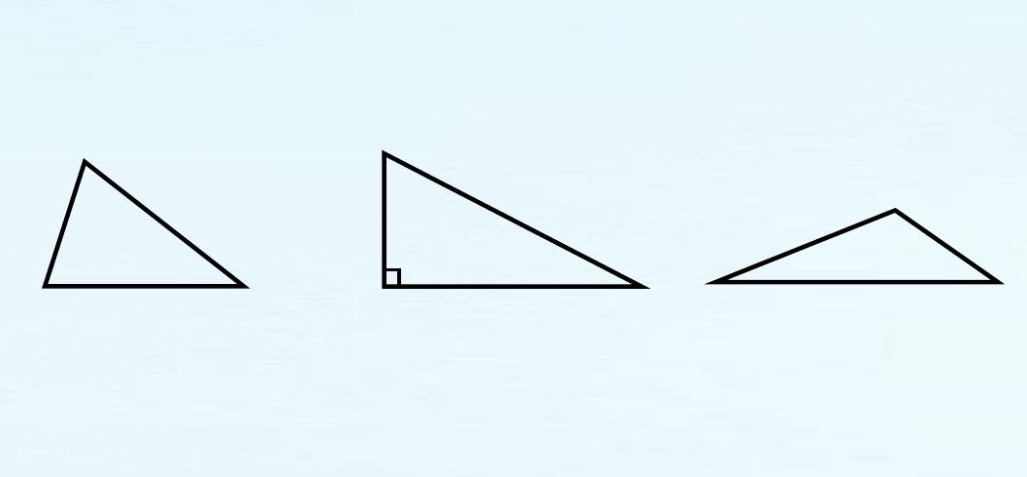
Types of Scalene Triangles:
While all scalene triangles have sides and angles of different lengths, they can be further classified based on their angles. The angles of a scalene triangle can be acute, obtuse, or right angles, leading to the following types:
Acute Scalene Triangle: In an acute scalene triangle, all three angles are less than 90 degrees. This type of triangle is the most common among scalene triangles.
Obtuse Scalene Triangle: An obtuse scalene triangle has one angle greater than 90 degrees. The other two angles are acute angles.
Right Scalene Triangle: A right scalene triangle contains one right angle, which measures exactly 90 degrees. The remaining two angles are acute angles.
Examples of Scalene Triangles:
Let's consider some examples to better understand scalene triangles:
Example 1: In a triangle with side lengths of 5 cm, 7 cm, and 9 cm, all sides are different lengths, making it a scalene triangle.
Example 2: A triangle with side lengths of 3 inches, 4 inches, and 6 inches is also a scalene triangle because none of its sides are equal.
Example 3: If a triangle has side lengths of 11 meters, 13 meters, and 15 meters, it is a scalene triangle because all three sides have different measures.
Facts about Scalene Triangles:
- Scalene triangles have three unequal sides and three unequal angles.
- The sum of the interior angles of a scalene triangle is always 180 degrees.
- Unlike equilateral or isosceles triangles, the angles of a scalene triangle can have any measure.
- Scalene triangles can be acute, obtuse, or right-angled, depending on the measures of their angles.
- The area of a scalene triangle can be calculated using various formulas, such as Heron's formula or the formula for the area of a triangle based on one side and its corresponding height.
Solved Examples on Scalene Triangle:
Let's solve a few examples related to scalene triangles to understand their properties and calculations better.
Example 1: Find the area of a scalene triangle with side lengths of 6 cm, 8 cm, and 10 cm.
Solution: To find the area of a scalene triangle, we can use Heron's formula, which states that the area (A) can be calculated as the square root of s(s-a)(s-b)(s-c), where s is the semi-perimeter and a, b, and c are the lengths of the sides.
In this case, the semi-perimeter (s) can be calculated as (6 + 8 + 10)/2 = 12 cm.
Now, substituting the values into the formula: Area (A) = √(12(12-6)(12-8)(12-10)) = √(1264*2) = √(576) = 24 cm²
Therefore, the area of the scalene triangle is 24 cm².
Example 2: Determine the type of triangle formed by the side lengths 2 inches, 3 inches, and 4 inches.
Solution: To determine the type of triangle, we need to examine the measures of the angles.
First, we can use the Law of Cosines to calculate one of the angles (A).
In this case, A = arccos((b² + c² - a²)/(2bc)) = arccos((3² + 4² - 2²)/(234)) ≈ arccos(0.375) ≈ 68.26 degrees
Similarly, we can calculate the other angles using the same formula.
B = arccos((a² + c² - b²)/(2ac)) ≈ arccos(0.625) ≈ 49.47 degrees
C ≈ 180 - (A + B) ≈ 62.27 degrees
Based on the measures of the angles, we can conclude that this triangle is an acute scalene triangle.
Practice Problems on Scalene Triangle:
Now, let's solve some practice problems to reinforce our understanding of scalene triangles.
Problem 1: Find the missing angle in a scalene triangle with angle measures of 40 degrees and 80 degrees.
Solution: To find the missing angle, we can use the fact that the sum of the angles in a triangle is always 180 degrees.
Let the missing angle be denoted as x.
40 degrees + 80 degrees + x = 180 degrees x = 180 degrees - 40 degrees - 80 degrees x = 60 degrees
Therefore, the missing angle in the scalene triangle is 60 degrees.
Problem 2: Calculate the perimeter of a scalene triangle with side lengths of 12 cm, 15 cm, and 18 cm.
Solution: The perimeter of a triangle is the sum of its side lengths.
Perimeter = 12 cm + 15 cm + 18 cm = 45 cm
Therefore, the perimeter of the scalene triangle is 45 cm.
Frequently Asked Questions on Scalene Triangle:
1. Can a scalene triangle have a right angle?
Yes, a scalene triangle can have a right angle, making it a right scalene triangle.
2. How many lines of symmetry does a scalene triangle have?
A scalene triangle does not have any lines of symmetry because its sides and angles are different.
3. What is the relation between the angles of a scalene triangle?
The angles of a scalene triangle are unequal and can have any measure, as long as their sum is 180 degrees.
4. What is the longest side in a scalene triangle?
The longest side in a scalene triangle can vary and is not necessarily fixed to a specific angle.
Conclusion:
A scalene triangle is a versatile and fundamental concept in geometry. Its distinctiveness lies in the fact that it has sides and angles of different lengths and measures. Whether acute, obtuse, or right-angled, scalene triangles offer various opportunities for mathematical exploration and problem-solving. Understanding their properties, calculations, and classifications enriches our knowledge of geometry and enhances our ability to solve real-world problems.