Associative Property
- What Is Associative Property in Math?
- Associative Property of Addition
- Associative Property of Multiplication
- Difference between Associative Property and Commutative Property
- Practice Problems On Associative Property
- Frequently Asked Questions On Associative Property
What Is Associative Property in Math?
The Associative Property is a fundamental concept in mathematics that applies to addition and multiplication. It states that the grouping of numbers being added or multiplied does not affect the result. In simple terms, it means that you can change the grouping of numbers without changing the outcome of the operation.
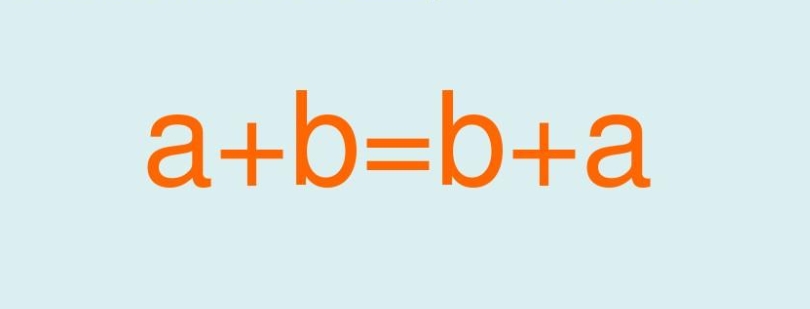
Associative Property of Addition:
The Associative Property of Addition states that for any three numbers a, b, and c, the sum of a and the sum of b and c is the same regardless of the grouping. Mathematically, it can be expressed as:
(a + b) + c = a + (b + c)
For example, let's take the numbers 2, 4, and 6. According to the Associative Property of Addition, the sum of (2 + 4) + 6 will be equal to 2 + (4 + 6). So, (2 + 4) + 6 equals 6 + 6, which equals 12. Similarly, 2 + (4 + 6) equals 2 + 10, which also equals 12. Therefore, the Associative Property holds true in this case.
Associative Property of Multiplication:
The Associative Property of Multiplication states that for any three numbers a, b, and c, the product of a and the product of b and c is the same regardless of the grouping. Mathematically, it can be expressed as:
(a x b) x c = a x (b x c)
Let's consider the numbers 3, 5, and 2. According to the Associative Property of Multiplication, the product of (3 * 5) * 2 will be equal to 3 * (5 * 2). So, (3 * 5) * 2 equals 15 * 2, which equals 30. Similarly, 3 * (5 * 2) equals 3 * 10, which also equals 30. Therefore, the Associative Property holds true in this case as well.
Difference between Associative Property and Commutative Property:
While the Associative Property and Commutative Property are both important concepts in mathematics, they are different from each other.
The Commutative Property states that the order of numbers being added or multiplied does not affect the result. Mathematically, it can be expressed as:
a + b = b + a (Commutative Property of Addition) a x b = b x a (Commutative Property of Multiplication)
In other words, you can change the order of numbers being added or multiplied without changing the outcome of the operation. For example, 2 + 3 is the same as 3 + 2.
On the other hand, the Associative Property focuses on the grouping of numbers being added or multiplied. It states that you can change the grouping of numbers without changing the outcome of the operation. For example, (2 + 3) + 4 is the same as 2 + (3 + 4).
Practice Problems On Associative Property:
Now, let's solve some practice problems to better understand the concept of the Associative Property.
Problem 1: Calculate the value of (2 + 5) + 8 and 2 + (5 + 8).
Solution: According to the Associative Property of Addition, both expressions will yield the same result.
(2 + 5) + 8 = 7 + 8 = 15 2 + (5 + 8) = 2 + 13 = 15
Therefore, both expressions are equal to 15.
Problem 2: Evaluate the value of (4 x 6) x 3 and 4 x (6 x 3).
Solution: According to the Associative Property of Multiplication, both expressions will yield the same result.
(4 x 6) x 3 = 24 x 3 = 72 4 x (6 x 3) = 4 x 18 = 72
Hence, both expressions are equal to 72.
Problem 3: Use the Associative Property of Addition to rearrange the expression (10 + 5) + 7.
Solution: According to the Associative Property of Addition, we can rearrange the expression as:
(10 + 5) + 7 = 10 + (5 + 7) = 10 + 12 = 22
Therefore, the rearranged expression is equal to 22.
Frequently Asked Questions On Associative Property:
1. Is the Associative Property applicable to subtraction and division as well?
No, the Associative Property is not applicable to subtraction and division. It only applies to addition and multiplication.
2. Can the Associative Property be used with more than three numbers?
Yes, the Associative Property can be used with any number of numbers. It states that the grouping of numbers being added or multiplied can be changed without affecting the result.
3. Can the Associative Property be used with negative numbers?
Yes, the Associative Property applies to both positive and negative numbers.
4. Can the Associative Property be used with decimals and fractions?
Yes, the Associative Property applies to decimals and fractions as well.
In conclusion, the Associative Property is a foundational concept in mathematics that applies to addition and multiplication. It states that the grouping of numbers being added or multiplied does not affect the result. The Associative Property of Addition states that the sum of a and the sum of b and c is the same regardless of the grouping, while the Associative Property of Multiplication states that the product of a and the product of b and c is the same regardless of the grouping. The Associative Property is different from the Commutative Property, which focuses on the order of numbers. The Associative Property is not applicable to subtraction and division, only to addition and multiplication. The property can be used with any number of numbers and applies to both positive and negative numbers, as well as decimals and fractions. By understanding and applying the Associative Property, mathematicians are able to simplify expressions and solve problems more efficiently.