30 60 90 Triangle
- What Is a “30-60-90” Triangle?
- 30-60-90 Triangle Rule
- Area of the 30-60-90 Triangle
- Solved Examples
- Practice Problems
- Frequently Asked Questions
What Is a “30-60-90” Triangle?
A 30-60-90 triangle is a special type of right triangle, where one of the angles measures 30 degrees, another angle measures 60 degrees, and the remaining angle is a right angle measuring 90 degrees. The sides of a 30-60-90 triangle are in a specific ratio, which makes it easy to calculate the lengths of the sides.
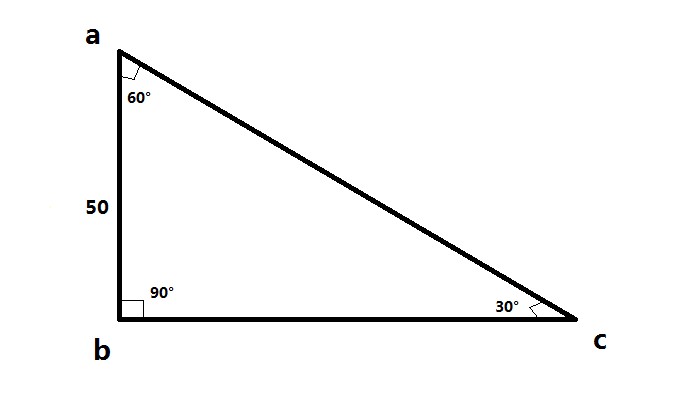
30-60-90 Triangle Rule:
The rule for a 30-60-90 triangle is that the ratio of the lengths of the sides is 1 : √3 : 2. This means that the side opposite the 30-degree angle is half the length of the hypotenuse, while the side opposite the 60-degree angle is the length of the hypotenuse multiplied by the square root of 3. Let's denote the hypotenuse as h, the side opposite the 30-degree angle as a, and the side opposite the 60-degree angle as b. Therefore, we have the following relationships:
a = h/2 b = h * √3
This rule allows us to easily find the lengths of the sides if we know the value of one side.
Area of the 30-60-90 Triangle:
To find the area of a 30-60-90 triangle, we can use the formula A = (1/2) * base * height. Since this triangle is a right triangle, the base and height can be any two sides that are perpendicular to each other. In a 30-60-90 triangle, the sides opposite the 30-degree and 60-degree angles can be considered as the base and height. Therefore, the formula for the area becomes:
A = (1/2) * b * a
Solved Examples:
Example 1: Find the lengths of the sides of a 30-60-90 triangle if the hypotenuse is 10 units.
Given: h = 10 units To find the length of the side opposite the 30-degree angle, we use the formula a = h/2: a = 10/2 = 5 units
To find the length of the side opposite the 60-degree angle, we use the formula b = h * √3: b = 10 * √3 ≈ 10 * 1.73 ≈ 17.32 units
Therefore, the lengths of the sides are a = 5 units, b ≈ 17.32 units, and h = 10 units.
Example 2: Find the area of a 30-60-90 triangle with side lengths 6 units and 12 units.
Given: a = 6 units, b = 12 units To find the area, we can use the formula A = (1/2) * b * a: A = (1/2) * 12 * 6 = 36 square units
Therefore, the area of the triangle is 36 square units.
Practice Problems:
- Find the lengths of the sides of a 30-60-90 triangle if the hypotenuse is 16 units.
- Find the area of a 30-60-90 triangle with side lengths 8 units and 16 units.
Frequently Asked Questions:
1. What is a 30-60-90 triangle?
A 30-60-90 triangle is a special type of right triangle with angles measuring 30 degrees, 60 degrees, and 90 degrees.
2. What is the rule for a 30-60-90 triangle?
The rule for a 30-60-90 triangle is that the ratio of the lengths of the sides is 1 : √3 : 2.
3. How do you find the lengths of the sides of a 30-60-90 triangle?
To find the lengths of the sides of a 30-60-90 triangle, you can use the rule that the side opposite the 30-degree angle is half the length of the hypotenuse, and the side opposite the 60-degree angle is the length of the hypotenuse multiplied by the square root of 3.
4. How do you find the area of a 30-60-90 triangle?
To find the area of a 30-60-90 triangle, you can use the formula A = (1/2) * b * a, where a and b are the sides opposite the 30-degree and 60-degree angles, respectively.
5. Can a 30-60-90 triangle have sides with decimal values?
Yes, a 30-60-90 triangle can have sides with decimal values. The ratio of the side lengths remains the same, regardless of whether the values are integers or decimals.
In conclusion
A 30-60-90 triangle is a special type of right triangle with angles measuring 30 degrees, 60 degrees, and 90 degrees. The sides of this triangle are in a specific ratio, which allows us to easily calculate their lengths. Additionally, the area of a 30-60-90 triangle can be found using the formula A = (1/2) * b * a. Understanding the properties and calculations related to 30-60-90 triangles is important in geometry and trigonometry, as they frequently appear in various mathematical problems and real-life applications.